Answer:
f(x) and g(x) are inverses
Step-by-step explanation:
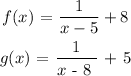
To find:
To determine whether f(x) and g(x) are inverses
For two function to be inverse of ech other, f(g(x))) = x and g(f(x)) = x. We will find the value/expression of f((g(x)) and g(f(x))
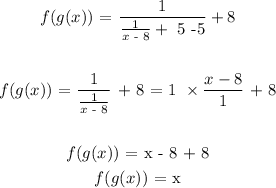

Since f(g(x)) = x and g(f(x)) = x
Then f(x) and g(x) are inverses