Question

State all integer values of x in the interval [-5,0] that satisfy the following inequality 4x+7>-9

Answer 1

• Integer values: ,numbers including 0, and negative and positive numbers; it can never be a fraction, a decimal, or a percent.

Based on the definition, the integer values included in the interval [-5, 0] are: -5, -4, -3, -2, -1, and 0.

To evaluate if the integer satisfies the inequality, we have to evaluate each integer.

• -5

`4\cdot(-5)+7>-9`
`-20+7>-9`
`-13>-9`

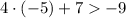
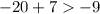
As -13 is smaller than -9, then -5 does not satisfy the inequality.

• -4

`4\cdot(-4)+7>-9`
`-16+7>-9`
`-9>-9`

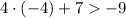
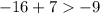
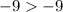
As -9 is equal to -9, then -4 does not satisfy the inequality (as in the sign of the inequality it is not included -9).

• -3

`4\cdot(-3)+7>-9`
`-12+7>-9`
`-5>-9`

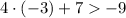
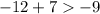
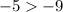
As -5 is bigger than -9, -3 satisfies the inequality.

• -2

`4\cdot(-2)+7>-9`
`-8+7>-9`
`-1>-9`

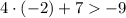
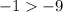
As -1 is bigger than -9, -2 satisfies the inequality.

• -1

`4\cdot(-1)+7>-9`
`-4+7>-9`
`3>-9`

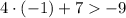
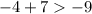
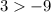
As 3 is bigger than -9, -1 satisfies the inequality.

• 0

`4\cdot(0)+7>-9`
`7>-9`

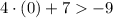
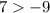
As 7 is bigger than -9, 0 satisfies the inequality.

Also we can try by solving the inequality:

`4x+7>-9`
`4x>-9-7`
`x>(-16)/(4)`
`x>-4`

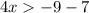
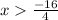
Meaning that all the values that are greater than -4 but not -4.

Answer:

• [-3, 0]

,

• x = -3, -2, -1, 0

,

• x > -4