Question

Graph the solution to the following inequality on the number line.(x - 2)(x-7)=0

Answer 1

We have the following expression:

`(x-2)\cdot(x-7)\leq0`

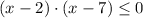
and we want to know the set of values of x that satisfies the inequality.

We see that in order to be the left-hand side of the inequality less or equal to zero we must have:

1) First case.

(x-2) is negative and (x-7) is positive, so its product is a negative number.

`\begin{gathered} (x-2)\leq0 \\ \text{and} \\ (x-7)\ge0 \end{gathered}`

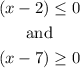
This is equivalent to have:

`\begin{gathered} x\leq2 \\ \text{and} \\ x\ge7 \end{gathered}`

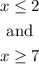
There are no values of x that can satisfy both inequalities at the same time. So this is an incompatible solution.

2) Second case

(x-2) is positive and (x-7) is negative, so its product is a negative number.

`\begin{gathered} (x-2)\ge0 \\ \text{and} \\ (x-7)\leq0 \end{gathered}`

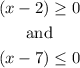
This is equivalent to have:

`\begin{gathered} x\ge2 \\ \text{and} \\ x\leq7 \end{gathered}`

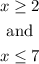
In this case, the inequalities are compatible and the set or range of values of x that satisfies these inequalities are:

`2\leq x\leq7`

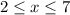
Plotting this in the graph: