ANSWER:
Magnitude is -120 and the direction is 60°
Explanation:
The unit vector is:
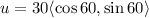
Let's call the new vector v, which would be:
v = -4u
The magnitude is calculated as follows:
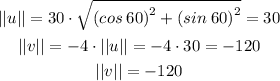
For the direction:
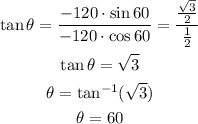
Which means that the magnitude is -120 and the direction is 60°