Question

To ensure proper water drainage, a landscaper needs to use 64 cubic meters of soil that is 31% sand. He has some soil that is 34% sand and some that is 28% sand. How much of each kind should he mix together?

Answer 1

Let x be the volume of 34% sand soil and y the volume of 28% sand soil, both in cubic meters.

The total volume of the mix is x+y. Then:

`x+y=64`

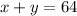
There is (34/100)x sand on the first mix and (28/100)y on the second mix. Together, they must account for a total of (31/100)*64 of sand. Then:

`(34)/(100)x+(28)/(100)y=(31)/(100)\cdot64`

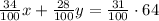
These two equations form a 2x2 system of equations. Solve it using the substitution method to find the volume of each mix that will be needed. To do so, isolate x from the second equation and substitute the resulting expression into the first one:

`\begin{gathered} (34)/(100)x+(28)/(100)y=(31)/(100)\cdot64 \\ \Rightarrow34x+28y=31\cdot64 \\ \Rightarrow34x=1984-28y \\ \Rightarrow x=(1984-28y)/(34) \end{gathered}`
`\begin{gathered} x+y=64 \\ \Rightarrow(1984-28y)/(34)+y=64 \\ \Rightarrow1984-28y+34y=64\cdot34 \\ \Rightarrow1984+6y=2176 \\ \Rightarrow6y=2176-1984 \\ \Rightarrow6y=192 \\ \Rightarrow y=(192)/(6) \\ \Rightarrow y=32 \end{gathered}`

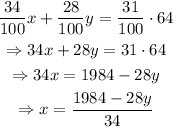
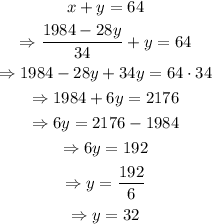
Substitute back y=32 into the first equation and solve for x:

`\begin{gathered} x+y=64 \\ \Rightarrow x+32=64 \\ \Rightarrow x=64-32 \\ \Rightarrow x=32 \end{gathered}`

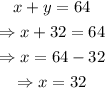
Therefore, 32 cubic meters of each kind of mix should be used.