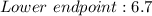Given that:
- A sample of children taken was:
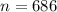
- The sample mean is:
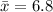
- The population standard deviation is:
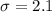
You know that you must construct the 85% confidence interval for the mean number of toys purchased each year.
Then, you need to use the Confidence Interval Formula for the Mean:
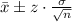
Where "z" is the critical value for confidence level, "n" is the sample size, σ is the standard deviation, and this is the sample mean:
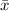
By definition the value of "z" for an 85% confidence interval is:
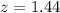
Therefore, by substituting values into the formula and evaluating, you get:
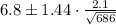
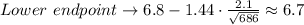
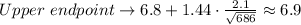
Hence, the answer is: