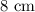Question

sing a ave Original Triangle Reduced Triangle 1 If a scale factor of is used to make a reduction, what 4 is the base of the reduced triangle? cm ah Height 24 cm Base 32 cm

Answer 1

We will investigtate the application of scale factors to re-size any image or figure.

The figure at hand is described as a triangle. Every triangle has two distinct side lengths namely:

`\text{Height \& Base}`

The original side-length for each of the distinct sides is given as follows:

`\begin{gathered} \text{Height : 24 cm} \\ \text{Base : 32 cm} \end{gathered}`

We are to re-size the original triangle as per the scale factor given:

`\text{Scale Factor = }(1)/(4)`

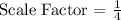
A general rule for re-sizing any figure either enlarging or shrinking can be given by the numerical value of scale factor as follows:

`\begin{gathered} \text{Scale Factor > 1 }\ldots\text{ Enlargement} \\ \text{Scale Factor = 1 }\ldots\text{ Actual/Original} \\ \text{Scale Factor < 1 }\ldots\text{ Shrinking/Reduction} \end{gathered}`

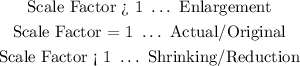
The scale factor given is expressed as a fraction (1/4). This lies in the third category. Hence, we will be reducing the size of the original triangle.

By re-sizing any figure we apply the scale factor to every distinct side-length of the figure. For the case of triangle these side lengths are base and height. The general formulation used while re-sizing is:

We will use the above relation for each of the side-lengths of a triangle as follows:

`\begin{gathered} \text{Reduced Height = }(1)/(4)\cdot24 \\ \\ \text{Reduced Height = 6 cm} \end{gathered}`
`\begin{gathered} \text{Reduced Base = }(1)/(4)\cdot32 \\ \\ \text{Reduced Base = 8 cm} \end{gathered}`

Therefore the base of the reduced triangle would be:

`8\text{ cm}`