Question

A community theater uses the function P(d) = -2d² + 100d-50 to model theprofit (in dollars) expected in a weekend when the tickets to a comedy show are priced at d dollars each.1) Write and solve an equation to find out the prices at which the theater would earn $750 in profit fromthe comedy show each weekend. Show your reasoning.2) At what price would the theater make the maximum profit, and what is that maximum profit?Show your reasoning.

Answer 1

`\begin{gathered} 1)\:Tickets:\$10\:\:and\:\$40 \\ 2)\:Price:\:\$25\:generates\:a\:maximum\:profit\:of\:\$1200 \end{gathered}`

1) In this first part, we need to find the value in which there is a revenue of $750.

`\begin{gathered} P(d)=-2d^2+100d-50 \\ 750=-2d^2+100d-50 \\ -2d^2+100d-50=750 \\ -2d^2+100d-800=0 \\ d_=(-100\pm√(100^2-4\left(-2\right)\left(-800\right)))/(2\left(-2\right)) \\ d_1=(-100+60)/(2\left(-2\right))=10,\:d_2=(-100-60)/(2\left(-2\right))=40 \\ d_1=10,d_2=40 \end{gathered}`

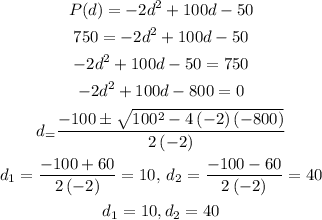
Notice that this is a quadratic equation so there are two points, i.e. prices in which the revenue will be $750. So, the tickets may cost $10 or $40 to yield a profit of $750.

2) To find the maximum profit (since this is an equation whose coefficient "a" is negative we need to find the vertex:

`\begin{gathered} V(h,k) \\ h=-(b)/(2a) \\ h=(-100)/(2(-2))=(-100)/(-4)=25 \\ \\ k=-2d^2+100d-50 \\ k=-2(25)^2+100(25)-50 \\ k=-2(625)+2500-50 \\ k=-1250+2500-50 \\ k=1200 \end{gathered}`

So, charging $25 generates a maximum profit of $1200

3) Thus, the answers are on the top.