Question

If a varies directly as the square of b, and a=5 when b=3, find a when b=2

Answer 1

We have that a varies directly as the square of b.

It means that when a increases, also b will increase.

Then, we can write the next equation:

`a=kb^2`

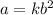
Where k is the constant of variation.

If a=5 when b=3

Then:

`\begin{gathered} 5=k(3)^2 \\ 5=k9 \\ \text{Solve for k:} \\ k=(5)/(9) \end{gathered}`

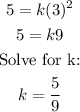
Now, we need to find the a value when b=2.

Hence:

`\begin{gathered} a=kb \\ a=k(2)^2 \\ \text{Where the contant k=(}(5)/(9)) \end{gathered}`

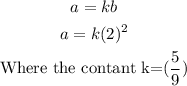
Replacing

`\begin{gathered} a=((5)/(9))2^2 \\ a=((5)/(9))4 \\ a=(20)/(9) \end{gathered}`

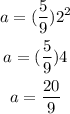
Therefore, when b=2, a value will be equal to 20/9.