Two companies A and B rent out trucks,
Company A charges $118 and allows unlimited mileage,
Company B charges an initial fee of $55 and $0.90 per mileage
Let m represent the number of miles,
Total fees for company B will be,
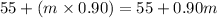
The expression to represent the mileage company A will charge less than company B can be given below in inequality form as,
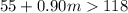
To find m, by collecting like terms above,

Since the number of miles company B must drive is 70 miles to have the exact charges as company A
Hence, at above 70 miles, company A will charge less than company B.