Let's see that the STP represents the conditions for the temperature of 0°C (273 K) and for the pressure of 1 atm.
We have this initial data and a volume of 3.20 x 10 ^(2) mL. To solve this problem, we need to use the ideal gas formula:
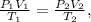
where T is temperature, P is pressure, and V volume. Subindex 1 is the initial data and subindex 2 is the final data.
We want to find the final volume, so clearing for V2 in the formula, we're going to obtain:
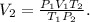
And the final step is replacing the data that we have, where the final data is 425.0 K and 3.50 atm (remember that the volume must be in liters, 1 liter is 1000 mL, so 3.20 x 10^2 mL is 0.32 L):
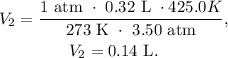
The answer is that the new volume of the sample of helium would be 0.14 L.