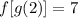To solve the exercise, first we are going to write the composition of the functions:
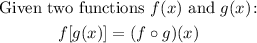
It reads "f composed of g", simply said "we are going to fill f with g":
So, in this case, we have
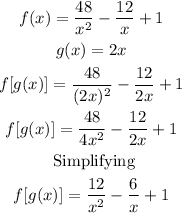
Now, we evaluate, that is, we replace x = 2 in the composite function and operate

Therefore,