Question

Juan deposited $4000 into an amount with 3.6% interest, compounded monthly. Assuming that no withdrawal are made, how much will he have in the account after 9 years? Round up to the nearest cent

Answer 1

Compound Interest

The final value of an investment of P dollars at an APR of r for t years is given by:

`FV=P\mleft(1+(r)/(m)\mright)^(m\cdot t)`

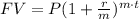
Where m is the number of compounding periods per year.

Juan deposited P = $4,000 into an account at r = 3.6% compounded monthly. Since there are 12 months in a year, m = 12.

Substituting for t = 9 years:

`FV=\$4,000\mleft(1+(0.036)/(12)\mright)^(12\cdot9)`

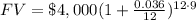
Calculating:

`\begin{gathered} FV=\$4,000(1+0.003)^(108) \\ FV=\$4,000(1.003)^(108) \\ FV=\$4,000\cdot1.381977 \\ FV=\$5,527.91 \end{gathered}`

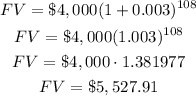
Juan will have $5,527.91 in the account