Question

Write an equation in slope-intercept form for the line that goes between these two points: (-4, 8) and (-2,7)

Answer 1

Step-by-step explanation:

To find the equation we must follow the following steps:

1.First we must find the slope with the points given by the exercise.

2.Then we have to find b, with one of those points.

3.Finally we replace the values ​​found in the equation for the slope.

The exercise is as follows:

Points: (-4, 8) and (-2, 7)

x1 y1 x2 y2

Now we must find the slope:

`\begin{gathered} m=(y2-y1)/(x2-x1) \\ m=(7-8)/(-2-(-4)) \\ m=(-1)/(2) \end{gathered}`

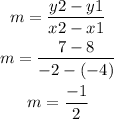
Now using one of the points of the exercise and with the slope, we substitute in the equation of the line to find b.The point we are going to use is:(-4, 8)

`\begin{gathered} y=mx+b \\ 8=(-1)/(2)(-4)+b \\ 8=(4)/(2)+b \\ 8=2+b \\ 8-2=b \\ 6=b \end{gathered}`

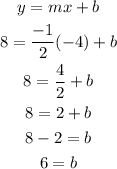
Since we already have b and the slope; now we can obtain the new equation of the line for the points given in the exercise; the equation is the following:

`\begin{gathered} y=mx+b \\ y=(-1)/(2)x+6 \\ \text{ANSWER :}the\text{ equation of the line is: y}=(-1)/(2)x+6 \end{gathered}`

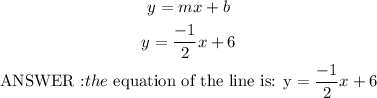
To check that it is ok, you have to give x values ​​in the equation to get b; for example if we give a vamor x of any of the given points, it should give us the same value in y.

`\begin{gathered} y=(-1)/(2)(-2)+6 \\ y=(2)/(2)+6 \\ y=1+6 \\ y=7 \\ \text{Then }for\text{ when }x\text{ is equal }to\text{ -2, y is equal }to\text{ 7} \end{gathered}`

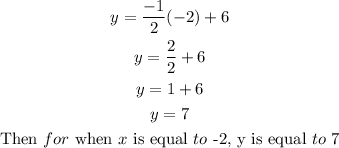
We can say that the exercise was perfectly well developed by verifying the equation.