Question

Poaching is causing a population of elephants to decline by 5% per year. Use the approximate half-lifeformula to determine the number that remains in 59 years if there are 8661 elephants today.

Answer 1

To find the half-life formula we will use the rule

`t_{(1)/(2)}=\frac{1}{\log _{(1)/(2)}(1-r)}`

Since the population of elephants decline by 5%, then

`\begin{gathered} r=(5)/(100) \\ r=0.05 \end{gathered}`

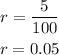
Then, substitute r in the rule above by 0.05

`\begin{gathered} t_{(1)/(2)}=\frac{1}{\log _{(1)/(2)}(1-0.05)} \\ t_{(1)/(2)}=\frac{1}{\log _{(1)/(2)}(0.95)} \\ t_{(1)/(2)}=13.5134\text{ years} \end{gathered}`

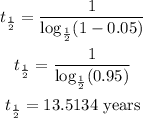
Now, to find the new value we will use the rule

`N=N_0((1)/(2))^{(t)/(t_(_0))_{}}`

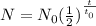
N(0) is the initial value

`N_0=8661`

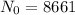
t is the time

`t=59`

Substitute these values in the rule above

`N=8661((1)/(2))^{(59)/(13.5134)}`

Find the answer

`N=420.0103933`

Round it to the whole number, then

The number of elephants will be 420