A linear equation is represented by the general form:
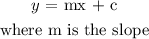
Required: We derive the equation using the given data and then compare their slopes
First, the graph has the following parameters

For the table, we pick two points/row data and then find the slope (m)
Let's use the first and second points i.e
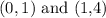
The equation to find the slope given two points is given as

By substituting:

Check: Which linear function has a greater slope?
Answer: none
Reason: slope for the equation represented by the graph is the same as that for the table.