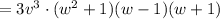Question

Factor completely3v^3w^4-3v^3

Answer 1

Answer: 3v² ( w²+1 )( w–1 )( w+1 )

`3v^2\left(w^2+1\right)\left(w-1\right)\left(w+1\right)`

Step-by-step explanation

Given

`3v^3w^4-3v^3`

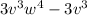
To factor it completely, we have to find the common factor between the two terms. In our case, it is 3v³:

`=3v^3\cdot(w^4-1)`

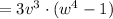
Next, we can further factorize the expression as a difference of squares, where:

`(x^2-a^2)=(x-a)(x+a)`

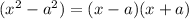
Applying this rule we get:

`=3v^3(w^2+1)\cdot(w^2-1)`

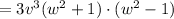
Finally, by applying the same rule as before but with the term (w² –1) we get:

`=3v^3\cdot(w^2+1)(w-1)(w+1)`