a)
The Rule of 72 states that the time required to double the investment (in years) is given by the formula below:
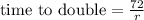
Where r is the investment rate in percentage.
So, for r = 5.6, we have:
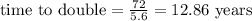
Therefore the time needed to double is 12.86 years.
b)
In order to calculate the exact time to double, let's use the formula below:

Where A is the final amount after t years, P is the principal (initial amount), r is the interest rate and n is how many times the interest is compounded in a year.
So, for A = 2P, r = 0.056 and n = 12, we have:

Therefore the time needed to double is 12.4 years.