Question

Find the perimeter and area of the sector for the figure shown in white, to three significant figures.

Answer 1

The area of a circle is computed as follows:

`A=\pi\cdot r^2`

If the radius is 7 cm, then the area is:

`A=\pi\cdot7^2=153.938\text{ sq. cm}`

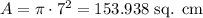
If the radius is 5 cm, then the area is:

`A=\pi\cdot5^2=78.539\text{ sq. cm}`

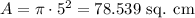
Then, the area of the "ring" made by the subtraction of a circle of a radius of 5 cm to a circle of a radius of 7 cm is:

153.938 - 78.539 = 75.399 sq. cm

In the picture of the problem, we see a part of this "ring". The whole area computed before corresponds to an angle of 360°, to calculate the area that corresponds to 120° we can use the next proportion:

`\begin{gathered} \frac{75.399\text{ sq. cm}}{x\text{ sq. cm}}=\frac{360\text{ \degree}}{120\text{ \degree}} \\ (75.399)/(x)=3 \\ (75.399)/(3)=x \\ 25.133\text{ sq. cm= x} \end{gathered}`

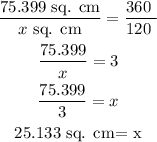
The perimeter of a circle is computed as follows:

`P=2\cdot\pi\cdot r`

If the radius is 7 cm, then the perimeter is:

`P=2\cdot\pi\cdot7=43.982\text{ cm}`

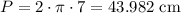
Given that 120° is 1/3 of a circle, then the length of the top arc is:

1/3*43.982 = 14.66 cm

If the radius is 5 cm, then the perimeter is:

`P=2\cdot\pi\cdot5=31.415\text{ cm}`

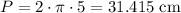
Given that 120° is 1/3 of a circle, then the length of the bottom arc is:

1/3*31.415 = 10.471 cm

Then, the perimeter of the figure is:

14.66 + 10.471 + 2 + 2 = 29.131 cm