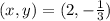We will solve the following system of equations by the addition method.
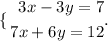
For doing so, we multiply the first and the second equation by some numbers, with the intention of making the coefficients of the variable x opposites.
Having this in mind, we will multiply the first equation for -7, using the distributive property.
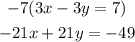
And the second equation by 3.
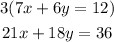
And we obtain,
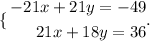
The next step is to sum both equations:
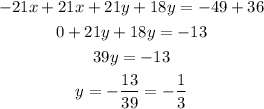
The last step is to replace the value on any of the two equations. We would do it on the first equation:
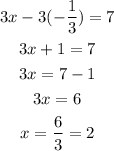
This means that the solution is: