Solution
A zombie infection in Tonky public schools grows by 15% per hour.
The formula for exponential growth is
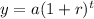
Where

The initial group of zombies was 4 freshman, i.e
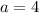
The growth rate, r is

The exponential growth equation is

After 14 hours, i.e t = 14 hours, the number of zombies there is

Hence, the number of zombies after 14 hours is 28 (nearest whole number)