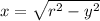Question

Let θ be an angle in quadrant II such that sin = 5/13.Find the exact values of secθ and tanθ .

Answer 1

Given:

sin θ = 5/13

θ is in Quadrant II

Find: sec θ and tan θ

Solution:

Recall that the sine function follows the pattern:

`sin\theta=(opposite)/(hypotenuse)=(y)/(r)`

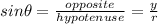
Therefore, from the given sin value, y = 5 and r = 13. Since the angle is found in quadrant II, the value of y is positive while the value of x should be negative.

Now, let's solve for the value of x using the formula below.

`x=√(r^2-y^2)`