Question

Classwork 1 - Week of 10/5 12-1 - Probability Events Murphy's math teacher sometimes wears scarves to class. Murphy has been documenting the relationship between his teacher wearing a scarf and when the class has a math quiz. The probabilities are as follows: P(wearing a scarf) = 10% P(math quiz) = 15% P(wearing a scarf and a math quiz) = 5% Are the events "the teacher is wearing a scarf" and "there will be a quiz" independent events? Explain.

Answer 1

In order to find out is the events are independent, we can check the following formula:

`P(A\cap B)=P(A)\cdot P(B)`

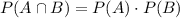
Where A is the event "the teacher is wearing a scarf" and B is the event "there will be a quiz", and P(A⋂B) is the probability of both events together.

If the result from the formula is true, the events are independent.

So using P(A) = 10%, P(B) = 15% and P(A⋂B) = 5%, we have:

`\begin{gathered} 0.05=0.1\cdot0.15 \\ 0.05=0.015\text{ (F)} \end{gathered}`

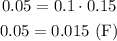
The result is false, that means the events are NOT independent (that is, they are dependent).