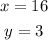We have the following system:

Solving by substitution method.
If we substitute equation A into B, we get
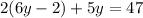
which gives
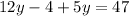
By combining similar terms, we have
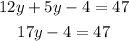
If we move -4 to the right hand side, we obtain
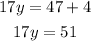
Then, if we move the coefficient of y to the right hand side, wehave
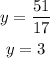
Then, we can substitute this result into equation A, which gives
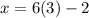
so, xi given by
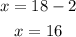
Therefore, the answer is