Question

Each of these is a pair of equivalent ratios for each pair explain why they are equivalent ratios.

Answer 1

Given the following set of ratios:

`4\colon5\text{ and 8:10}`
`18\colon3\text{ and 6:1}`

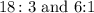
To be able to determine if the given sets are equivalent ratios, they must a common constant, k, which is x/y.

`\text{ k = }(x)/(y)`

Let's treat the ratio as x:y and find their common constant, k.

At 4:5 and 8:10,

`k_(4\colon5)\text{ = }(4)/(5)`
`k_(8\colon10)\text{ =}(8)/(10)\text{ = }((8)/(2))/((10)/(2))\text{ = }(4)/(5)\text{ ; simplified}`

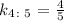
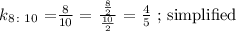
Since the two ratios have the same common constant, k = 4/5, the two ratios are equivalent.

At 18:3 and 6:1,

`\text{ k}_(18\colon3)\text{ = }(18)/(3)\text{ = }((18)/(3))/((3)/(3))\text{ = }(6)/(1)\text{ = 6}`
`\text{ k}_(6\colon1)=(6)/(1)\text{ = 6}`

Since the two ratios have the same common constant, k = 6, the two ratios are equivalent.