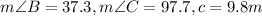Answer:
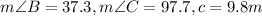
Step-by-step explanation:
Given:
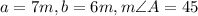
The given side is the longer of the two, so there will be only one solution.
Using Law of Sines:
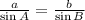
Substitute the given values:
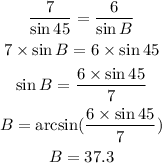
The sum of the angles in a triangle is 180 degrees.
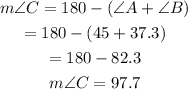
Finally, we find the length of c using the Sine rule.
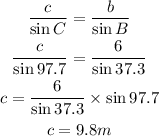
Thus, the solution to the triangle is: