Answer:
4 m/s
Step-by-step explanation:
By the conservation of momentum, we can write the following equation
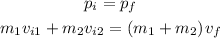
Where pi is the initial momentum and it is equal to the sum of the mass times the velocity of the person and the sled. pf is the final momentum of the person and the sled.
The sled is initially stationary, so its initial velocity vi2 is 0 m/s.
We need to know the final velocity vf, so solving for vf, we get
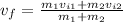
Now, we can replace m1 = 80 kg, vi1 = 5 m/s, m2 = 20 kg, vi2 = 0 m/s to get
![\begin{gathered} v_f=\frac{(80\operatorname{kg})(5\text{ m/s)+(20kg)(0 m/s)}}{80\operatorname{kg}+20\operatorname{kg}} \\ v_f=\frac{400\operatorname{kg}\text{ m/s+0 kg m/s}}{100\operatorname{kg}} \\ v_f=\frac{400\operatorname{kg}\text{ m/s}}{100\operatorname{kg}\text{ m/s}} \\ v_f=4\text{ m/s} \end{gathered}]()
Therefore, the speed of the person and the sled after the landing is 4 m/s
slp