The direction of 12 m is towards west north with an angle of 20 with the y-axis or north.
The direction of 20 m is towards the south west with an angle of 40 with the x-axis or west.
From the given figure,
The angle between the 12 m and the west is,
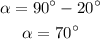
Thus, the angle between the 12 m and 20 m is,
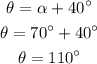
The resultant of the 12 m walk and 20 m walk is,
![R=\sqrt[]{A^2+B^2+2AB\cos (\theta)}](https://img.qammunity.org/2023/formulas/physics/college/9p13thvgwh63gtosavew4qwdm6aderdzx3.png)
Substituting the known values,
![\begin{gathered} R=\sqrt[]{12^2+20^2+2*12*20*\cos (110^(\circ))} \\ R=19.5\text{ m} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/12am11u9nsafcm0yke8jt706xul0jzwuhf.png)
Thus, the magnitude of the resultant of R is 19.5 m.