Question

62. A(4, -1) and B(-2, 3) are points in a coordinate plane. Mis the midpoint of AB.What is the length of MB to the nearest tenth of a unit?HC

Answer 1

Ok, so:

We know that A(4, -1) and B(-2, 3) are points in a coordinate plane. M is the midpoint of AB.

We want to find the length of MB.

M is the midpoint of AB, which is:

`\begin{gathered} ((-2+4)/(2),(3-1)/(2)) \\ (1,1) \end{gathered}`

Remember that if we've got two points:

`(x_1,y_1);(x_2,y_2)`

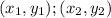
The distance between them can be found using the formula:

`D=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}`

We want to find the length of MB, this is the distance between M( 1 , 1 ) and B( -2 , 3 ).

Replacing:

`\begin{gathered} D=\sqrt[]{(3-1)^2+(-2-1)^2} \\ D=\sqrt[]{2^2+(-3)^2} \\ D=\sqrt[]{4+9} \\ D=\sqrt[]{13} \\ D=3.61 \end{gathered}`

Therefore, the length of MB is 3.61.