Question

Find the values of y and x.*2 pointsCaptionless ImageA) y = 5, x = 10B) y = 10, x = 5C) y = 5, x = 5√2D) y = 10, x = 5√3

Answer 1

Given that there is a right-angled triangle having the two sides as x and y and the third side is 5 units.

Also one of the angles is 45 degrees.

Explanation -

Here we will use the trigonometric formulae taking into consideration the angle 45.

Then, we know

`\begin{gathered} tan\theta=(Perpendicular)/(Base) \\ and\text{ cos}\theta=(Base)/(Hypotenuse) \\ Also\text{ tan45=1 and cos45=}(1)/(√(2)) \end{gathered}`

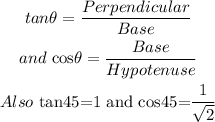
For a 45-degree angle, the base is y, the perpendicular is 5 and the hypotenuse is x.

Then,

`\begin{gathered} tan45=(5)/(y) \\ 1=(5)/(y) \\ y=5 \\ and\text{ cos45=}(y)/(x) \\ (1)/(√(2))=(5)/(x) \\ x=5√(2) \end{gathered}`

So the values of x and y are 5√2 and 5 respectively and hence the option C is correct.

Therefore the final answer is y = 5 and x = 5√2