Question

Determine if the graph is symmetric above the x-axis the y-axis or the originr=-5-5costheta

Answer 1

Step 1: Test for symmetry about the x-axis by Replacing θ with -θ in the equation

The curve r=f(θ) is symmetrical about the x-axis if the equation r=f(θ) is unchanged by replacing θ with -θ

`r=5-5\cos (-\theta)=5-5\cos \theta\text{ (}\cos (-\theta)=\cos \theta)`

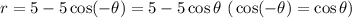
Hence, the curve is symmetrical about the x-axis

Step 2 Test for symmetry about the y-axis by Replacing θ with -θ and r with -r in the equation

The curve r=f(θ) is symmetrical about the x-axis if the equation r=f(θ) is unchanged by replacing θ

with -θ and r with -r

`\begin{gathered} -r=5-5\cos (-\theta)=5-5\cos \theta \\ \text{ Therefore} \\ r=-5+5\cos \theta \\ \text{ Since } \\ -5+5\cos \theta\\e5-5\cos \theta \\ \text{ then there is no symmetry about the y-axis} \end{gathered}`

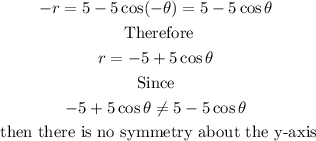
Step 2 Test for symmetry about the origin by replacing r with -r in the equation

The curve r=f(θ) is symmetrical about the origin if the equation r=f(θ) is unchanged by replacing r

with -r

`\begin{gathered} -r=5-5\cos \theta \\ \text{this implies that} \\ r=-5+5\cos \theta \\ \text{ Since} \\ -5+5\cos \theta\\e5-5\cos \theta \\ \text{ then there is no symmetry about the origin} \end{gathered}`

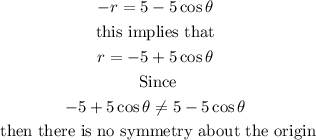
Therefore, the curve is symmetrical only about the x-axis.

Hence, the right option is the first one.