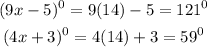Answer:
121 degrees and 59 degrees respectively.
Step-by-step explanation:
The sketch of the roads is attached below:
If Sycamore Street and Rosewood Street both intersect Main Street at the same angle, it means the angle labeled a above is equal to (9x-5) degrees.
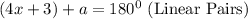
Since a=(9x - 5) degrees.
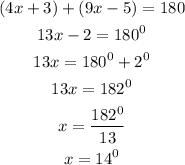
Therefore, the measure of the given angles these streets makes with Main Street are: