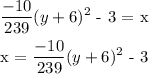Step 1:
If you have the equation of a parabola in vertex form

then the vertex is at (h,k) and the focus is (h,k+14a). Notice that here we are working with a parabola with a vertical axis of symmetry, so the x-coordinate of the focus is the same as the x-coordinate of the vertex.
Step 2:
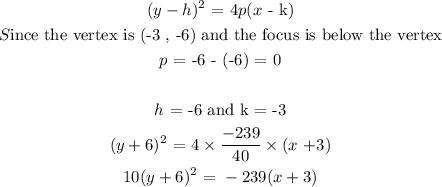
Step 3
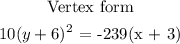
Step 4:
In standard form