To determine which expression gives as a result 3/4 you have to solve them:
When you divide two fractions, you have to invert the denominator of the division (reciprocal fraction) and multiply the numerator of the division by the reciprocal fraction.
a.

Reverse the denominator
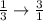
And multiply both fractions
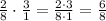
Both 6 and 8 are divisible by 2, so you can simplify the result as
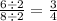
b.
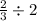
Determine the reciprocal of the denominator
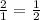
And multiply it by the numerator of the division
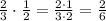
Both values are divisible by 2, so you can simplify the result as:
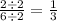
c.
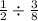
Determine the reciprocal fraction
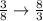
Multiply both fractions
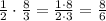
Divide the numerator and denominator by 2 to simplify the fractions
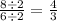
d.
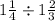
Express both mixed fractions as improper fractions


So the division is
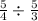
Determine the reciprocal fraction
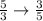
And multiply both fractions
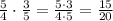
Both values 15 and 20 are divisible by 5, you can simplify the result
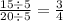
e.
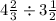
Convert the fractions from mixed to improper


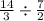
Determine the reciprocal fraction
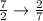
And multiply both fractions
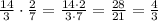
From the given quotients, those that have 3/4, as a result, are "a." and "d."