Given the equation:
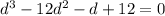
To solve the equation for d, follow the steps below.
Step 01: Factor by grouping.
To factor by grouping, group the polynomial into two sections.
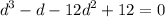
First group: d³ - d.
Second group: -12d² + 12.
The first group has "d" in common, while the second group has 12 (or -12) in common. To, factor out these values and write the expression again.
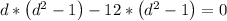
Factor out (d² - 1).
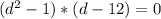
Step 02: Solve for d.
In order for the product to be zero, the first term or the second group must be zero.
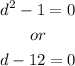
Solving the first equation:
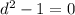
Adding 1 to both sides and then taking the square root.

Solving the second equation:
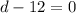
Adding 12 to both sides:
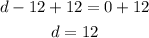
Answer: d = -1, 1, 12.