Question

Find length of BD and then use that answer to find m angle CDB (round to the nearest tenth)

Answer 1

• BD = 19.3

,

• m∠CDB = 68.7°

Explanation:

In right triangle ABD:

• The side length ,opposite to, A, 47 degrees = BD

,

• The side length ,adjacent to, A = AB = 18

Using trigonometric ratios:

`\begin{gathered} \tan A=\frac{\text{opposite}}{\text{Adjacent}} \\ \implies\tan 47\degree=(BD)/(18) \end{gathered}`

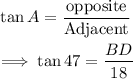
Cross multiply:

`\begin{gathered} BD=18*\tan 47\degree \\ BD=19.3 \end{gathered}`

Next, in triangle BCD:

• The length of the ,hypotenuse, BD = 19.3

,

• The side length, adjacent angle D = CD = 7

From trigonometric ratios:

`\begin{gathered} \cos D=(CD)/(BD) \\ \cos D=(7)/(19.3) \\ D=\arccos ((7)/(19.3)_{}) \\ D=68.7\degree \end{gathered}`

Therefore, the measure of angle CDB is 68.7 degrees (correct to the nearest tenth).