Question

Please help need help with what are the complex zero of f(x). Of the equation below I sent an image.

Answer 1

We have to find all the complex zeros of f(x), defined as:

`f(x)=7x^4-6x^3+174x^2-150x-25`

We have no direct method to find the zeros for a fourth degree polynomial.

We can try to factorize the polynomial by looking at common factors between the coefficients.

We can factorize the coefficients as:

`\begin{gathered} 7=7 \\ 6=3\cdot2 \\ 174=29\cdot3\cdot2 \\ 150=5^2\cdot3\cdot2 \\ 25=5^2 \end{gathered}`

If we test for y = f(1) we obtain y = 0, meaning that x = 1 is a root of the polynomial.

If we divide f(x) by (x-1) we obtain:

`(7x^4-6x^3+174x^2-150x-25)/(x-1)=7x^3+x^2+175x+25`

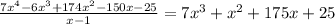
As 175/25 = 7 we can use this to factorize the rest of the polynomial as:

`\begin{gathered} 7x^3+x^2+175x+25 \\ x^2(7x+1)+25(7x+1) \\ (x^2+25)(7x+1) \end{gathered}`

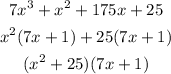
The factor 7x+1 indicates that x = -1/7 is another (real root).

The factor x²+25 can not be factorized any further with real coefficients, so it corresponds to complex roots.

For polynomials with real coefficients, the complex roots come in conjugate pairs.

In this case, we can find the complex roots as:

`\begin{gathered} x^2+25=0 \\ x^2=-25 \\ x=√(-25) \\ x=√(5^2(-1)) \\ x=\pm5√(-1) \\ x=\pm5i \end{gathered}`

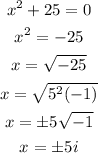
Then, the complex roots for f(x) are 5i and -5i.

Answer: -5i, 5i