1. Surface area:
We need to split trinagular prism into 5 different polygons. Then calculate the area for each of them, and finally add up the five results to find the total surface area.
We have 2 triangles and 3 rectangles.
Both triangles are equal, so, we only need to find the area for one of them:
- Triangle:
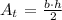
We know h (h = 5 in), but we don't know b, and here is where the Pythagorean theorem comes in:
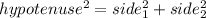
For our trinagle, we know the hypotenuse length (13 in) and one side length (5 in), so:
![\begin{gathered} \text{missing}_{}\text{ side = }\sqrt[]{hypotenuse^2-side^2_1} \\ \text{missing}_{}\text{ side = }\sqrt[]{13^2-5^2} \\ \text{missing}_{}\text{ side = }\sqrt[]{169\text{ - 25}}\text{ = }\sqrt[]{144}\text{ = 12} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/2xyecbe3t5ysugdo6kny1686ondhcg1mn3.png)
And so, going back to the triangle area, we have:
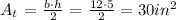
- "Front" rectangle area:
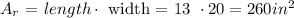
- "Right" rectangel area:
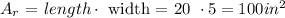
- "Left" rectangle area:
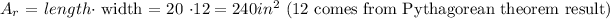
Finally, the surface area of the triangle prism is:
30 + 30 + 260 + 100 + 240 = 660 in^2
2. Volume
The volume is just the area of the base triangle times the height of the prism. So:
