Question

Diseases tend to spread according to the exponential growth model. In the early days of AIDS, the rate of growth of the disease was around 90 percent per year. In 1983, about 1500 people in the U.S. died of AIDS. If the trend had continued unchecked, how many people would have died from AIDS in 1994?

Answer 1

To compute how many people would have died from AIDS in 1994, we will use this formula,

`\text{ Growth Rate = }(\frac{People\text{ died in 1994}}{People\text{ died in 1983}})^{(1)/(n)}\text{ - 1}`

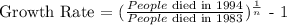
Where,

n = years between 1994 and 1983.

Growth Rate = 90% = 90%/100% = 0.90

People died in the year 1983 = 1500

People died in the year 1994 = unknown

Let's compute for n,

`\text{ n = 1994 - 1983 = 11}`

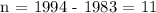
Let,

x = people would have died from AIDS in 1994

We get,

`\text{ Growth Rate = }(\frac{People\text{ died in 1994}}{People\text{ died in 1983}})^{(1)/(n)}\text{ - 1}`
`\text{ 0.90 = (}(x)/(1500))^{(1)/(11)}\text{ - 1}`
`\text{ 1500 (0.90 + 1)}^(11)\text{ = x}`
`\text{ x = (1500)(1164.90) = 1,747,350}`

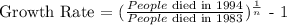
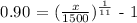
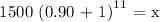
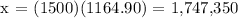
1,747,350 people would have died from AIDS in the year 1994.