Question

If the sum of the interior angle measures of a polygon is 2340 degrees, then what kind of polygon is it?

Answer 1

Pentadecagon

Explanation

The sum of the interior angle measures (in degrees) of a regular polygon is:

`\text{ sum of interior angles }=(n-2)\cdot180`

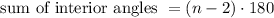
where n is the number of sides of the polygon.

Substituting with sum of interior angles = 2340° and solving for n:

`\begin{gathered} 2340=(n-2)\cdot180 \\ (2340)/(180)=((n-2)\cdot180)/(180) \\ 13=n-2 \\ 13+2=n-2+2 \\ 15=n \end{gathered}`

This number of sides corresponds to a pentadecagon.