We have the next system of equations
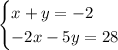
And we must solve it by combining the equations.
To solve it by combining the equation we need to add up the two equations trying to delete one of the variables
So, we can add 2*E1 + E2 (E1 represents equation 1 and E2 represents equation 2)
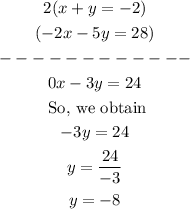
Now, since we know y = -8, we can replace it in equation 1 and then solve it for x
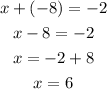
Finally, we obtatin x = 6 and y = -8
ANSWER:
x = 6, y = -8