Question

What is the next term of the geometric sequence?-5, -10, -20, -40,...

Answer 1

EXPLANATION

Compute the general progression formula of -5, -10, -20, -40,...

Check whether the ratio is constant:

-5, -10, -20, -40,...

Compute the ratio of all the adjacent terms:

`r=(a_(n+1))/(a_n)`

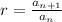
-10/-5=2, -20/-10=2, -40/-20=2

The ratio of all the adjacent terms is equal to 2.

The first element of the sequence is a_1=-5

By definition, the formula is given by the expression:

`a_n=a_1\cdot r^(n-1)`

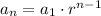
Therefore the nth term is computed by

r=2, a_n= -5*2^(n-1)

The next term is a_5

Compute a_5

`a_5=-5\cdot2^(5-1)`

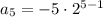
So,

`a_(5=-80)`

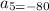
The next term is -80.