Question

The diameter of a cylindrical water tank is 12ft and it’s height is 9ft. What is the volume of the tank? Use the value 3.14 for pie and round your answer to the nearest whole number. Be sure to include the correct unit in your answer

Answer 1

The Solution:

The given figure is:

`V=\pi r^2h`

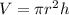
First, we shall find the value of the radius of the cylinder.

`\begin{gathered} =(d)/(2) \\ \text{ where} \\ r=\text{radius}=\text{?} \\ d=\text{diameter}=12\text{ ft} \\ \text{ So,} \\ \text{Substituting 12 for d, we get} \\ r=(12)/(2)=6\text{ ft} \end{gathered}`

To find the volume of the given cylindrical tank above, we shall use the formula below:

`V=\pi r^2h`

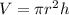
In this case,

`\begin{gathered} \pi=3.14\text{ (given)} \\ r=\text{radius}=6\text{ ft} \\ h=\text{height}=9ft \\ V=Volume=? \end{gathered}`

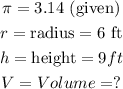
Substituting these values in the formula above, we get

`V=3.14*6^2*9=3.14*36*9=1017.36\approx1017ft^2`

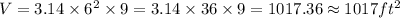
Therefore, the correct answer is 1017 squared feets