ANSWER
Arithmetic sequence. Common difference: (t - s)
Step-by-step explanation
The terms for a geometric sequence has this form:
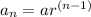
So a = a1. In this case a = s. If this sequence were geometric, the second term should involve s. Therefore, it's not geometric.
The terms for an arithmetic sequence are:
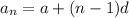
The first term is also a = a1. In tihs case, the first term is s, so a = s
Assuming this is an arithmetic sequence, a2 = t. With this we can look for d, the common difference:
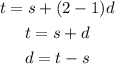
If d = (t-s), then the third term is:
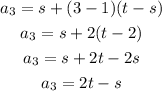
Which is the same as the 3rd term of the given sequence. Therefore this is an arithmetic sequence and the common difference is (t - s)