Question

Please see attached photo for my problem. Thanks in advance. These are homework practice sets.

Answer 1

a.

The total cost of any business include the fixed cost and the variable cost. Let x be the number of sandwiches made and sold, the total cost per week is given by:

`C(x)=\text{ (variable cost)}x+(\text{ fixed cost)}`

Plugging the values given in the problem we have that the total cost function is:

`C(x)=1.90x+2480`

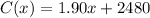
b.

The revenue is equal to the number of units sold multiplied by the price per unit, that is:

`R(x)=x\cdot p(x)`

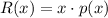
plugging the price function we have that:

`\begin{gathered} R(x)=x(9.50-0.003x) \\ R(x)=9.50x-0.003x^2 \\ R(x)=-0.003x^2+9.50x \end{gathered}`

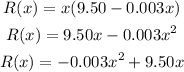
Therefore the revenue function is:

`R(x)=-0.003x^2+9.50x`

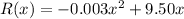
c.

The profict function is defined as the revenue function minus the cost function, then:

`\begin{gathered} P(x)=R(x)-C(x) \\ P(x)=-0.003x^2+9.50x-(1.90x+2480) \\ P(x)=-0.003x^2+7.60x-2480 \end{gathered}`

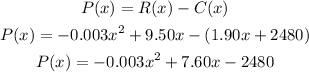
Therefore the profict function is:

`P(x)=-0.003x^2+7.60x-2480`

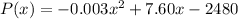
d.

The break even point happens when the revenue function and the cost function are equal or, in other words, when the profit function is equal to zero, then to find the break even point we have to solve the equation:

`-0.003x^2+7.60x-2480=0`

We can solve this equation by the general formula method or we can graph functions C(x) and R(x) to find the intersections, let's use the second method:

The graphs of the cost and revenue functions are shown below:

From it we notice that the break even points are x=384.75 and x=2148.584.

e.

To determine the level of sales that maximizes the profit we can graph the profit function to find its maximum value; the graph of the profit function is:

From it we conclude that the level of sales that maximizes it is 1266.667 and that the maximum profit is $2333.33 (in the maximum profit we rounded to the cents of a dollar)

f.

To determine the price that maximizes the profit we use the value we found in the previous point for x in the price function, then we have:

`\begin{gathered} p=9.50-0.003(1266.667) \\ p=5.6999 \\ p\approx5.7 \end{gathered}`

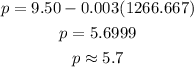
Therefore the price that maximizes the profit is $5.70 (rounded to cents)