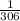
Step-by-step explanation
Two events are dependent when the outcome of the first event influences the outcome of the second event. The probability of two dependent events is the product of the probability of X and the probability of Y AFTER X occurs
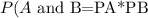
now, the probability of an event is t is the number of favorable outcomes divided by the total number of outcomes possible.

Step 1
find the probabily of each event
A)event: first presentation kelly
let
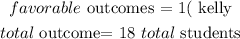
now, replace
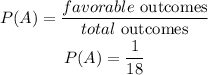
b) event b, Harmony second presentation
let
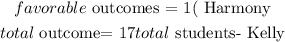
hence
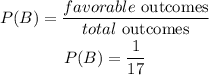
Step 2
finally, do the producto of the probabilities
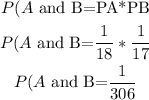
therefore, the answer is
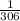
I hope this helps you