Question

Can you lease help me!! Only solve the problem that says 1A but identify what it says!

Answer 1

If the relation between the number of revolutions made by a tire and the radius of the tire varies inversely, then, you can write:

`y=(k)/(x)`

where y is the number of revolutions, x the radius and k the constant of proportionality.

Based on the given information, you can calculate the value of k, as follow:

If x = 12 (radius in inches) and y = 100 (revolutions), then, by solving for k, you get:

`k=yx=(100)(12)=1200`

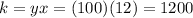
Then, the relation between x and y can be written as follow:

`y=(1200)/(x)`

Now, if the radius of the tire is x = 16, then, the number of revolutions to travel the same distance is:

`y=(1200)/(16)=75`

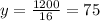
In this case, the defined variables are:

x: radius of the tire

y: number of revolutions of the tire

k: constant variation = 1200