Answer: (2x+3y) and (x-y)
Given:
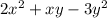
We can factor the given expression by grouping. We can rewrite the following expression:
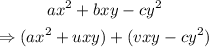
Given that:
a = 2
b = 1
c = -3
uv = ac
uv = 2(-3)
uv = -6
*Factor -6:
u = -2
v = 3
We now have:

We can now factor the expression easily:

Therefore, its factors would be (2x+3y) and (x-y)