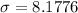To find the standard deviation:
From the given table values,
Sum of the squared deviation is,
222.6064+166.9264+119.2464+98.4064+98.4064+79.5664+35.0464+8.5264+
3.6864+3.6864+0.8464+0.8464+0.0064+0.0064+0.0064+0.0064+4.3264+
4.3264+82.4464+82.4464+101.6064+145.9264+145.9264+145.9264+121.0864=1671.84.
The formula for standard deviation is,
![\sigma=\sqrt[]{\frac{\sum^{}_{}(x-\mu)^2}{N}}](https://img.qammunity.org/2023/formulas/mathematics/college/hjvnj6nr3hmzuu1qbaj0qe3eo80fw02lnj.png)
Here, N=25
So we have,
![\begin{gathered} \sigma=\sqrt[]{(1671.84)/(25)} \\ =\sqrt[]{66.8736} \\ =8.1776 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8twqlnuhhir4kta67dd3mhm2g21o5ajo1j.png)
Hence the standard deviation is,