Answer:
23. 63 degrees
Step-by-step explanation:
Let us draw a free body diagram.
The net forces on ladder + painter must equal zero. Therefore, along the y-direction:
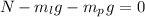
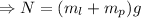
Along the x-direction
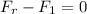
Now, we calculate the torque about the about O.
The torque is must be zero:
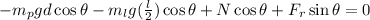
simplifying the above gives
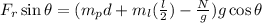
Since
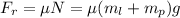
the above becomes
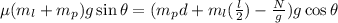
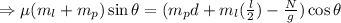
dividing both sides by cosine gives
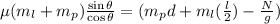
further division gives
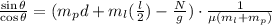
substitute the value of N and we get:
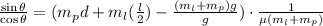
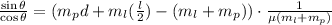
putting in m_p = 60 kg, m_l = 10 kg, l = 6.0 m and d = 1/3 * 6 = 2, and u = 0.5 gives,
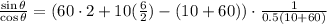
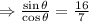
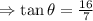
taking the inverse tan of both sides gives
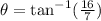
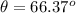
Therefore, the required angle against the wall is
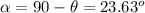
Hence, the ladder should lean 23.63 degrees against the wall.